I have been interacting with my statistician colleagues lately and there was a reporting requirement to calculate medians over a spread of continuously distributed values. Thankfully with SQL Server 2012, you do not have to use the ROW_NUMBER() function as you had to with earlier T-SQL versions.
PERCENTILE_CONT and PERCENTILE_DISC are now available in T-SQL 2012. According to the SQL BOL, these functions are described as:
PERCENTILE_CONT: Calculates a percentile based on a continuous distribution of the column value in SQL Server 2012. The result is interpolated and might not be equal to any of the specific values in the column.
PERCENTILE_DISC: Computes a specific percentile for sorted values in an entire rowset or within distinct partitions of a rowset in SQL Server 2012. PERCENTILE_DISC calculates the percentile based on a discrete distribution of the column values; the result is equal to a specific value in the column.
Let us put these functions to test and understand them a bit more in detail:
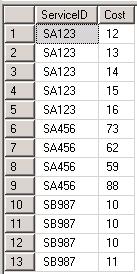
I have a sample table(ServiceCost) with ServiceIDs (that will be the data element to group by) and Cost (the field for which medians have to be calculated).
I calculated the medians using PERCENTILE_CONT and PERCENTILE_DISC as below:
</code> SELECT DISTINCT ServiceID, PERCENTILE_CONT(0.5) WITHIN GROUP (ORDER BY Cost) OVER (PARTITION BY ServiceID) AS MedianValue, PERCENTILE_DISC(0.5) WITHIN GROUP (ORDER BY Cost) OVER (PARTITION BY ServiceID) AS MedianDisc FROM ServiceCost order by ServiceID<code>
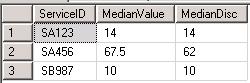
The result of this query is:
The difference between the way these two functions work is clear from the output for ServiceID: SA456. The PERCENTILE_CONT function calculated the mean of the values {62,73} to result in 67.5; while the PERCENTILE_DISC function resulted in the value 62 which is one of the column values in the data set.
We can now show off the power of T-SQL for statistical analysis… Hurray!